Reflection law
To find out the optimal path of light, we must first assume that A A
A B B B x x x
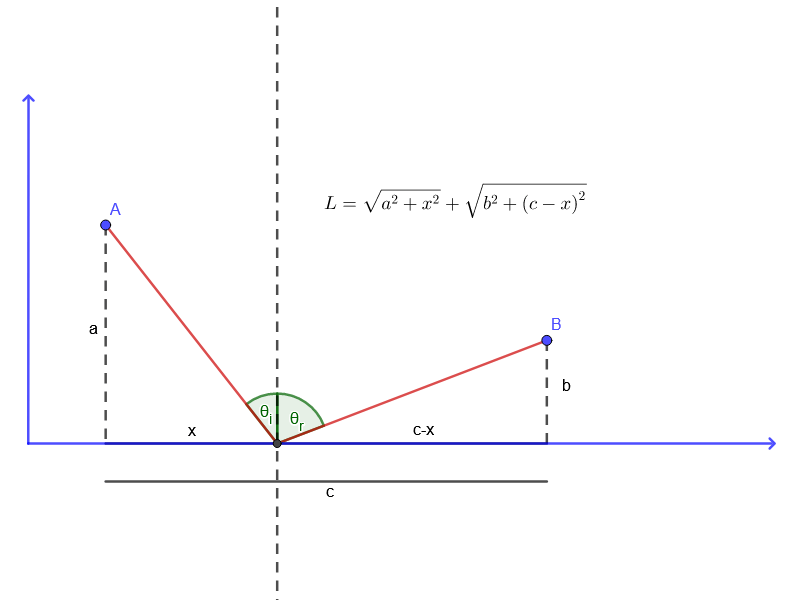
The path length from A A A B B B
L ( x ) = a 2 + x 2 + b 2 + ( c − x ) 2 L \left( x \right) = \sqrt{a^{2} + x^{2}} + \sqrt{b^{2} + \left( c -
x \right)^{2}} L ( x ) = a 2 + x 2 + b 2 + ( c − x ) 2
Since the velocity is constant, the path in minimum time is simply the
path of minimum distance. This can be calculated by taking the
derivative of L L L x x x
L ′ ( x ) = 1 2 2 x a 2 + x 2 + 1 2 2 ( c − x ) ( − 1 ) b 2 + ( c − x ) 2 = x a 2 + x 2 − ( c − x ) b 2 + ( c − x ) 2 = 0 \begin{split}L^{\prime} \left( x \right) &= \frac{1}{2}
\frac{2x}{\sqrt{a^{2} + x^{2}}} + \frac{1}{2} \frac{2 \left( c - x
\right) \left( -1 \right)}{\sqrt{b^{2} + \left( c - x \right)^{2}}} \\
& = \frac{x}{\sqrt{a^{2} + x^{2}}} - \frac{ \left( c - x \right)
}{\sqrt{b^{2} + \left( c - x \right)^{2}}} = 0 \end{split} L ′ ( x ) = 2 1 a 2 + x 2 2 x + 2 1 b 2 + ( c − x ) 2 2 ( c − x ) ( − 1 ) = a 2 + x 2 x − b 2 + ( c − x ) 2 ( c − x ) = 0
But we can notice in the previous image
sin θ i = x a 2 + x 2 sin θ r = c − x b 2 + ( c − x ) 2 \begin{split} \sin\theta_{i} &= \frac{x}{\sqrt{ a^{2} + x^{2} }} \\
\sin\theta_{r} &= \frac{c - x}{\sqrt{b^{2} + \left(c - x\right)^{2}}}
\end{split} sin θ i sin θ r = a 2 + x 2 x = b 2 + ( c − x ) 2 c − x
that way we can rewrite the above equation as
sin θ i − sin θ 2 = 0 ⇔ sin θ i = sin θ 2 , \begin{split}&\sin\theta_{i} - \sin\theta_{2} = 0 \\ \Leftrightarrow
&\sin\theta_{i} = \sin\theta_{2}, \end{split} ⇔ sin θ i − sin θ 2 = 0 sin θ i = sin θ 2 ,
equivalently it is
θ i = θ r , \theta_{i} = \theta_{r}, θ i = θ r ,
which is the Reflection Law.
Instructions
Move the green slider to change angle of incidence.
See also
Path optimization
Differential calculus
Mirrors
Optics formulas
